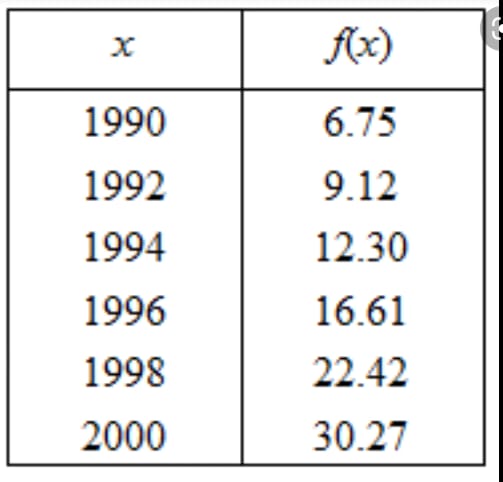
Week 5: Differential. Growth and decay model. ( page 224, Exercise 3.7 , Exercise 3.8)

The differential of a function is equal to the derivative of the function times the differential of the independent variable: dy=df(x)=f′(x)dx. The key concept of exponential growth is that the population growth rate —the number of organisms added in each generation—increases as the population gets larger. When population size, N, is plotted over time, a J-shaped growth curve is made.Systems that exhibit exponential growth follow a model of the form y=y0ekt. In exponential growth, the rate of growth is proportional to the quantity present. In other words, y′=ky. Decay models are applicable on data sets where data items are associated with points in a metric space (locations) and there is a notion of “significance” of a data item to a location, which decays (decreases) with the distance between the item and the location. This decrease is modeled by a decay function.

Download Files

stewart-calculas.pdf (32.22 MB )