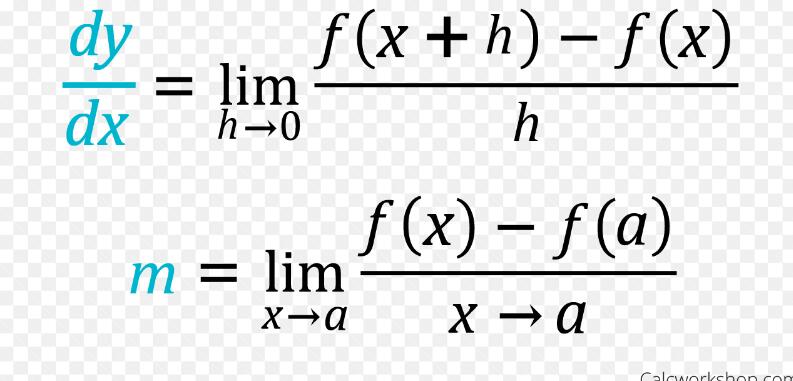
week 1: Functions, Domain and Range of Functions, The vertical line test, The limit of functions, Graph of functions, Definition of derivative.

A function is a mapping from a set of inputs (the domain) to a set of possible outputs (the codomain). The definition of a function is based on a set of ordered pairs, where the first element in each pair is from the domain and the second is from the codomain.      The vertical line test is used to determine if a graph of a relationship is a function or not. if you can draw any vertical line that intersects more than one point on the relationship, then it is not a function.

A limit tells us the value that a function approaches as that function's inputs get closer and closer to some number. The idea of a limit is the basis of all calculus.One-Sided Limits (Formal) Limit from the Right: Let f(x) be defined over an open interval of the form (a,b) where a0, there exists a δ>0, such that if 0Limits and derivatives are extremely crucial concepts in Maths whose application is not only limited to Maths but are also present in other subjects like physics.  The complete concepts of limits and derivatives along with their properties, and formulas are discussed. We will cover the important formulas, properties and examples questions to understand the concept of limits as well as derivatives in detail. In mathematics (particularly in differential calculus), the derivative is a way to show instantaneous rate of change: that is, the amount by which a function is changing at one given point. For functions that act on the real numbers, it is the slope of the tangent line at a point on a graph.

Download Files

stewart-calculas.pdf (32.22 MB )