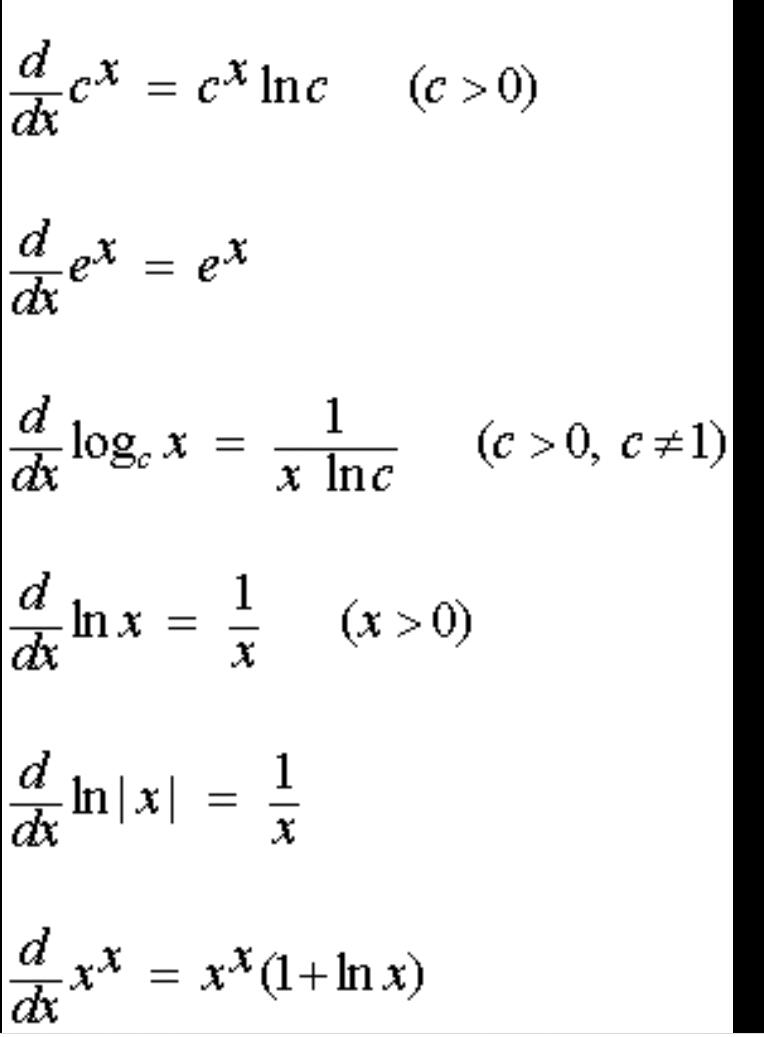
Week 3: Derivative of logarithmic Exponential and Trigonometric Functions. ( Exercise 3.2 , Exercise 3.3)
On the page Definition of the Derivative, we have found the expression for the derivative of the natural logarithm function y=lnx: (lnx)′=1x. Now we consider the logarithmic function with arbitrary base and obtain a formula for its derivative. Δy=loga(x+Δx)−logax. Note that the exponential function f( x) = e x has the special property that its derivative is the function itself, f′( x) = e x = f( x).
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions[1][2]) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis.
The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent. Their reciprocals are respectively the cosecant, the secant, and the cotangent, which are less used.
Download Files
- week 1: Functions, Domain and Range of Functions, The vertical line test, The limit of functions, Graph of functions, Definition of derivative.
- week 2: The derivatives and results of Differentiation. ( Exercise 2.8 and Exercise 3.1)
- Week 3: Derivative of logarithmic Exponential and Trigonometric Functions. ( Exercise 3.2 , Exercise 3.3)
- Week 4: Derivative of algorithmic, exponential and Trigonometry functions. Curve Sketching. Application of derivatives in Business and Economics.
- Week 5: Differential. Growth and decay model. ( page 224, Exercise 3.7 , Exercise 3.8)
- Week 6: Limits and Continuity. The derivatives
- Week 7: Definite and indefinite integrals. Techniques of integration. (page 372 to 382, Exercise 5.2))
- Week 8: Integration
- Week 9: Mid Term
- Week 10: Using integral in finding Areas
- Week 11: Area between curves
- Week 12: integration by part
- Week 13: Integral involving Logarithmic, Exponential and Trigonometric Functions.
- Week 14: Integration by Tables. Area under a curve and between curves
- Week 15: Functions of several variables, Partial derivatives and their applications to optimization.
- Week 16: Infinite Series
- Week 17: Differential Equation
- Week 18: Final term
- Chapters 18
- Department Noon Business School
- Teacher
Ms. Iqra Anum
