Week7 Differentiation of Polynomials and rational functions

Tecniques to find Derivative of Polynomuials and rational functions

Polynomials are some of the simplest functions we use. We need to know the derivatives of polynomials such as x4+3x, 8x2+3x+6, and 2. Let's start with the easiest of these, the function y=f(x)=c, where c is any constant, such as 2, 15.4, or one million and four (106+4). It turns out that the derivative of any constant function is zero. This makes sense if you think about the derivative as the slope of a tangent line. To use the definition of a derivative, with f(x)=c,

 

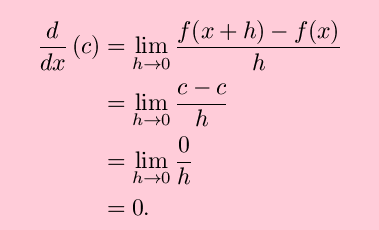
For completeness, now consider y=f(x)=x. This is the equation of a straight line with slope 1, and we expect to find this from the definition of the derivative. We are not disappointed:

 

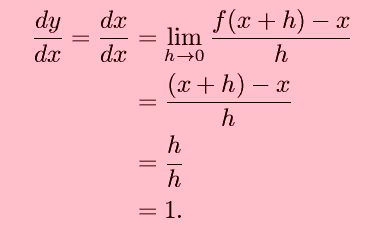
Two things to note in the above:

  • It may be tempting to ``cancel'' the term ``dx'' in the intermediate step. This is valid, but only in this simple case.
  • It will never be as easy as this again, although it won't be much harder.

    Before going to the most general case, consider y=f(x)=x2. This is the most basic parabola, as shown. The derivative of f(x) may still be found from basic algebra: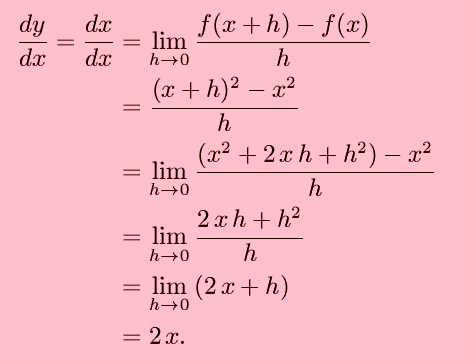

     

    This tells us exactly what we expect; the derivative is zero at x=0, has the same sign as x, and becomes steeper (more negative or positive) as x becomes more negative or positive.

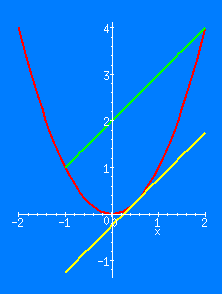    An interesting result of finding this derivative is that the slope of the secant line is the slope of the function at the midpoint of the interval. Specifically,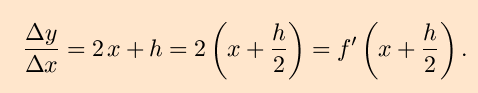

     

    (In the figure shown, x = -1 and h = 3, so (x+h/2) = +1/2.
    Please note that parabolic functions are the only functions (aside from linear or constant functions) for which this is always true.

    From here, we can and should consider y=f(x)=xn for any positive integer n. There are many ways to do this, with varying degrees of formality.

    To start, consider that for n a positive integer, the binomial theorem allows us to express f(x+h) as

     

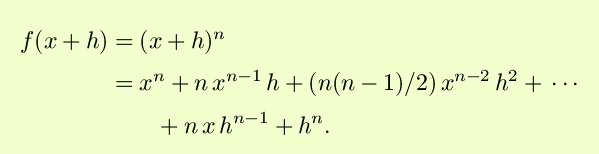
    (In the above, there will always be no more than n+1 nonzero terms.) Then, algebra again gives us

     

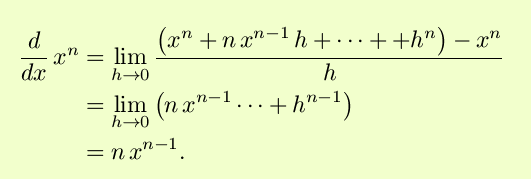
    This very convenient form is seen to reproduce the above results for n=1, n=2 and even n=0, which is the case c=1.
    The above result could be found from an inductive process, using the product rule, but the inductive step is similar to that which allows extension of the binomial theorem to all positive integers, and adds little to this presentation.

    The extension from f(x)=xn to arbitrary polynomials (only finite order will be considered here) needs only two straightforward, perhaps even obvious results:

     

    • The derivative of the sum of two function is the sum of the derivatives.
    • The derivative of a function multiplied by a constant is the derivative of the fuctnion multiplied by the same constant.

    In symbols, these results are

     

     

     

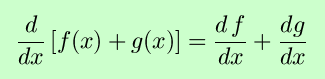
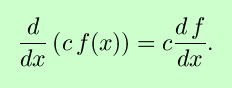
    In the above, c is a constant, and differentiability of the functions at the desired points is assumed.

    Combining all of these results, we can see that for the coefficients ak all constants,

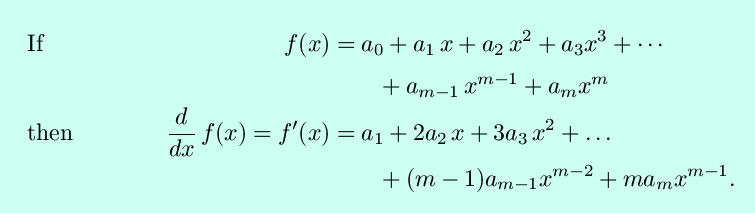
    This is often seen in summation notation as

     

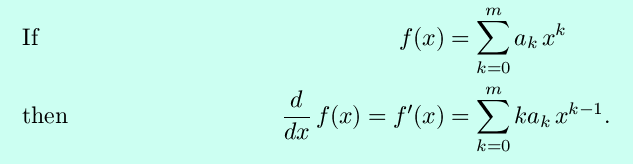
    Examples

    •  


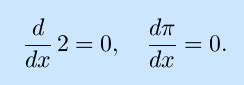
      These are just the derivatives of constants, and hence both zero.
    •  


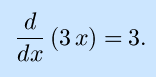
      That is, the derivative of the function that describes a line with slope 3 is indeed that same slope, 3.
    •  

    •  


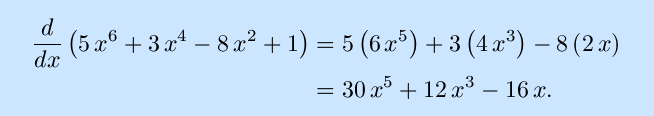
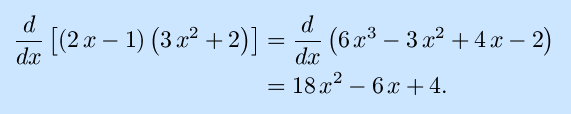
      And there's no reason that the variable x is special:
    •  

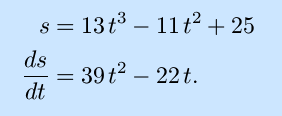
    Exercises:

    Find the derivative with respect to x of the following functions: