Week 1 Introduction to numbers
The Real Number System
The real number system evolved over time by expanding the notion of what we mean by the word “number.” At first, “number” meant something you could count, like how many sheep a farmer owns. These are called the natural numbers, or sometimes the counting numbers.
Natural Numbers
or “Counting Numbers”
1, 2, 3, 4, 5, . . .
- The use of three dots at the end of the list is a common mathematical notation to indicate that the list keeps going forever.
At some point, the idea of “zero” came to be considered as a number. If the farmer does not have any sheep, then the number of sheep that the farmer owns is zero. We call the set of natural numbers plus the number zero the whole numbers.
Whole Numbers
Natural Numbers together with “zero”
0, 1, 2, 3, 4, 5, . . .
About the Number ZeroWhat is zero? Is it a number? How can the number of nothing be a number? Is zero nothing, or is it something? Well, before this starts to sound like a Zen koan, let’s look at how we use the numeral “0.” Arab and Indian scholars were the first to use zero to develop the place-value number system that we use today. When we write a number, we use only the ten numerals 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. These numerals can stand for ones, tens, hundreds, or whatever depending on their position in the number. In order for this to work, we have to have a way to mark an empty place in a number, or the place values won’t come out right. This is what the numeral “0” does. Think of it as an empty container, signifying that that place is empty. For example, the number 302 has 3 hundreds, no tens, and 2 ones. So is zero a number? Well, that is a matter of definition, but in mathematics we tend to call it a duck if it acts like a duck, or at least if it’s behavior is mostly duck-like. The number zero obeys most of the same rules of arithmetic that ordinary numbers do, so we call it a number. It is a rather special number, though, because it doesn’t quite obey all the same laws as other numbers—you can’t divide by zero, for example. Note for math purists: In the strict axiomatic field development of the real numbers, both 0 and 1 are singled out for special treatment. Zero is the additive identity, because adding zero to a number does not change the number. Similarly, 1 is the multiplicative identity because multiplying a number by 1 does not change it.
|
Even more abstract than zero is the idea of negative numbers. If, in addition to not having any sheep, the farmer owes someone 3 sheep, you could say that the number of sheep that the farmer owns is negative 3. It took longer for the idea of negative numbers to be accepted, but eventually they came to be seen as something we could call “numbers.” The expanded set of numbers that we get by including negative versions of the counting numbers is called the integers.
Integers
Whole numbers plus negatives
. . . –4, –3, –2, –1, 0, 1, 2, 3, 4, . . .
About Negative NumbersHow can you have less than zero? Well, do you have a checking account? Having less than zero means that you have to add some to it just to get it up to zero. And if you take more out of it, it will be even further less than zero, meaning that you will have to add even more just to get it up to zero. The strict mathematical definition goes something like this: For every real number n, there exists its opposite, denoted – n, such that the sum of n and – n is zero, or n + (– n) = 0 Note that the negative sign in front of a number is part of the symbol for that number: The symbol “–3” is one object—it stands for “negative three,” the name of the number that is three units less than zero. The number zero is its own opposite, and zero is considered to be neither negative nor positive. Read the discussion of subtraction for more about the meanings of the symbol “–.”
|
The next generalization that we can make is to include the idea of fractions. While it is unlikely that a farmer owns a fractional number of sheep, many other things in real life are measured in fractions, like a half-cup of sugar. If we add fractions to the set of integers, we get the set of rational numbers.
Rational Numbers
All numbers of the form 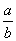 , where a and b are integers (but b cannot be zero)
, where a and b are integers (but b cannot be zero)
Rational numbers include what we usually call fractions
- Notice that the word “rational” contains the word “ratio,” which should remind you of fractions.
The bottom of the fraction is called the denominator. Think of it as the denomination—it tells you what size fraction we are talking about: fourths, fifths, etc.
The top of the fraction is called the numerator. It tells you how many fourths, fifths, or whatever.
- RESTRICTION: The denominator cannot be zero! (But the numerator can)
If the numerator is zero, then the whole fraction is just equal to zero. If I have zero thirds or zero fourths, than I don’t have anything. However, it makes no sense at all to talk about a fraction measured in “zeroths.”
- Fractions can be numbers smaller than 1, like 1/2 or 3/4 (called proper fractions), or they can be numbers bigger than 1 (called improper fractions), like two-and-a-half, which we could also write as 5/2
All integers can also be thought of as rational numbers, with a denominator of 1:
The Real Number System
The real number system evolved over time by expanding the notion of what we mean by the word “number.” At first, “number” meant something you could count, like how many sheep a farmer owns. These are called the natural numbers, or sometimes the counting numbers.
Natural Numbers
or “Counting Numbers”
1, 2, 3, 4, 5, . . .
- The use of three dots at the end of the list is a common mathematical notation to indicate that the list keeps going forever.
At some point, the idea of “zero” came to be considered as a number. If the farmer does not have any sheep, then the number of sheep that the farmer owns is zero. We call the set of natural numbers plus the number zero the whole numbers.
Whole Numbers
Natural Numbers together with “zero”
0, 1, 2, 3, 4, 5, . . .
About the Number ZeroWhat is zero? Is it a number? How can the number of nothing be a number? Is zero nothing, or is it something? Well, before this starts to sound like a Zen koan, let’s look at how we use the numeral “0.” Arab and Indian scholars were the first to use zero to develop the place-value number system that we use today. When we write a number, we use only the ten numerals 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. These numerals can stand for ones, tens, hundreds, or whatever depending on their position in the number. In order for this to work, we have to have a way to mark an empty place in a number, or the place values won’t come out right. This is what the numeral “0” does. Think of it as an empty container, signifying that that place is empty. For example, the number 302 has 3 hundreds, no tens, and 2 ones. So is zero a number? Well, that is a matter of definition, but in mathematics we tend to call it a duck if it acts like a duck, or at least if it’s behavior is mostly duck-like. The number zero obeys most of the same rules of arithmetic that ordinary numbers do, so we call it a number. It is a rather special number, though, because it doesn’t quite obey all the same laws as other numbers—you can’t divide by zero, for example. Note for math purists: In the strict axiomatic field development of the real numbers, both 0 and 1 are singled out for special treatment. Zero is the additive identity, because adding zero to a number does not change the number. Similarly, 1 is the multiplicative identity because multiplying a number by 1 does not change it.
|
Even more abstract than zero is the idea of negative numbers. If, in addition to not having any sheep, the farmer owes someone 3 sheep, you could say that the number of sheep that the farmer owns is negative 3. It took longer for the idea of negative numbers to be accepted, but eventually they came to be seen as something we could call “numbers.” The expanded set of numbers that we get by including negative versions of the counting numbers is called the integers.
Integers
Whole numbers plus negatives
. . . –4, –3, –2, –1, 0, 1, 2, 3, 4, . . .
About Negative NumbersHow can you have less than zero? Well, do you have a checking account? Having less than zero means that you have to add some to it just to get it up to zero. And if you take more out of it, it will be even further less than zero, meaning that you will have to add even more just to get it up to zero. The strict mathematical definition goes something like this: For every real number n, there exists its opposite, denoted – n, such that the sum of n and – n is zero, or n + (– n) = 0 Note that the negative sign in front of a number is part of the symbol for that number: The symbol “–3” is one object—it stands for “negative three,” the name of the number that is three units less than zero. The number zero is its own opposite, and zero is considered to be neither negative nor positive. Read the discussion of subtraction for more about the meanings of the symbol “–.”
|
The next generalization that we can make is to include the idea of fractions. While it is unlikely that a farmer owns a fractional number of sheep, many other things in real life are measured in fractions, like a half-cup of sugar. If we add fractions to the set of integers, we get the set of rational numbers.
Rational Numbers
All numbers of the form 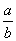 , where a and b are integers (but b cannot be zero)
, where a and b are integers (but b cannot be zero)
Rational numbers include what we usually call fractions
- Notice that the word “rational” contains the word “ratio,” which should remind you of fractions.
The bottom of the fraction is called the denominator. Think of it as the denomination—it tells you what size fraction we are talking about: fourths, fifths, etc.
The top of the fraction is called the numerator. It tells you how many fourths, fifths, or whatever.
- RESTRICTION: The denominator cannot be zero! (But the numerator can)
If the numerator is zero, then the whole fraction is just equal to zero. If I have zero thirds or zero fourths, than I don’t have anything. However, it makes no sense at all to talk about a fraction measured in “zeroths.”
- Fractions can be numbers smaller than 1, like 1/2 or 3/4 (called proper fractions), or they can be numbers bigger than 1 (called improper fractions), like two-and-a-half, which we could also write as 5/2
All integers can also be thought of as rational numbers, with a denominator of 1:


