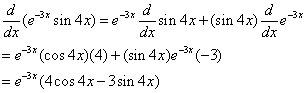week 8 Derivative of transcisdental functions

Lecture 1

We find derivatives of trigonometric functions by using following

Lecture 2

Derivatives of Inverse Trigonometric Functions

lecture 3

Derivatives Exponential Functions

In general, an exponential function is of the form

f(x) = ax where a is a positive constant.

Derivative of the Natural Exponential Function

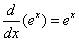
The exponential function f(x) = ex has the property that it is its own derivative. This means that the slope of a tangent line to the curve y = ex at any point is equal to the y-coordinate of the point.

We can combine the above formula with the chain rule to get

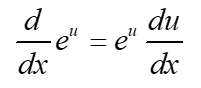
Example:

Differentiate the function y = e sin x

Solution:

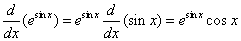
Example:

Differentiate the function y = e–3xsin4x

Solution:

Using the Product Rule and the above formulas, we get

 

Download Files

20200506-200852.jpg (1.02 MB )

20200506-200907.jpg (0.95 MB )

20200506-200928.jpg (1.05 MB )

20200506-201005.jpg (1.04 MB )

20200506-201016.jpg (1.07 MB )

20200506-201027.jpg (0.96 MB )